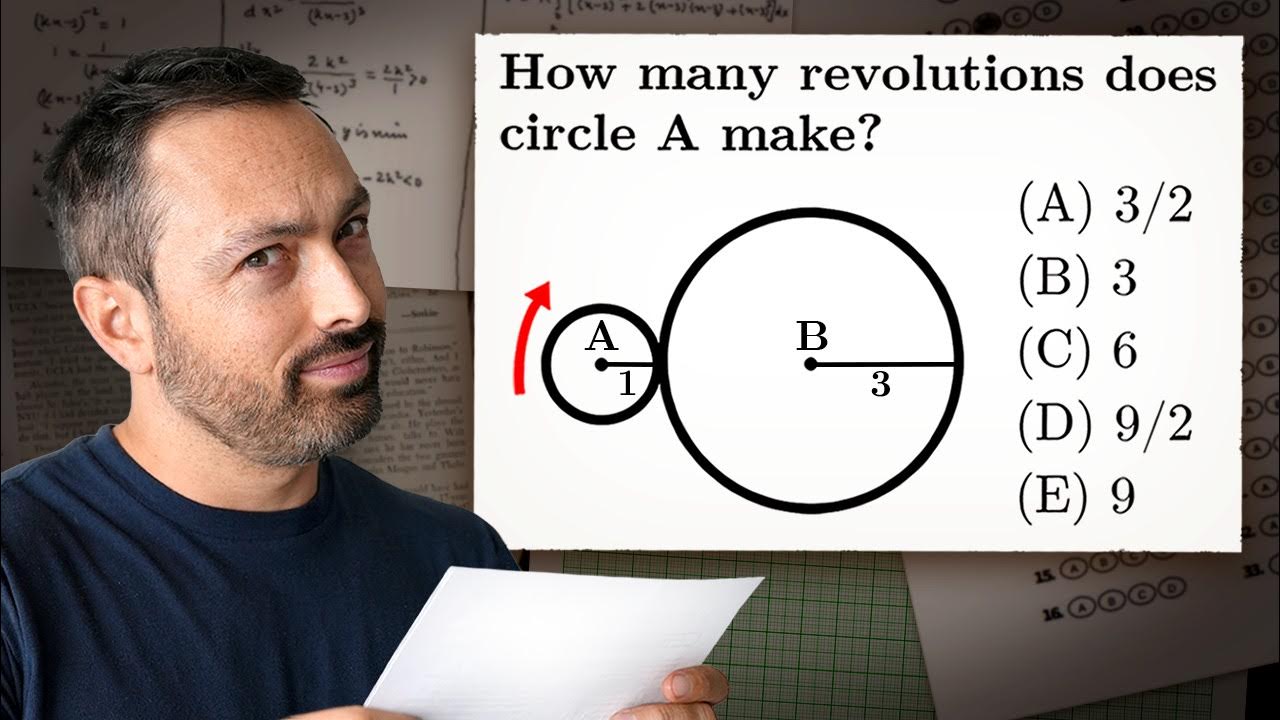For anyone still struggling with the intuition:
How many times does a circle rotate if you roll it around a tiny dot? 1
How many times does it rotate if you roll it around another circle the same size? Gotta be more than the dot, right?
I would’ve never gotten that! I started getting lost trying to think about the differences in circumferences and radii before they mentioned the right or wrong answers
My only intuition was this: if you take two identical coins and rotate them together (like a pair of gears), it takes one rotation each to reach the starting point. If you now rotate your head along with one of the coins, it will appear standing still, while the other one will be rotating twice as fast.
I still would have guessed the answer was 6, though. It took me awhile to figure out how extrapolate this model to a 3:1 ratio. As it turns out, it still works, and you get 4, but evidence of that was far from obvious to me.
I probably would have gotten four because I would have visually saw the answer without knowing the equation.
I bet you would have discovered gravity first if only the apple fell on your head instead of pesky Newton
Lots of people saw gravity in action, Newton figured out the equation.
I don’t think that’s a brag.
Assuming they did what I did, they saw it and went ‘no fucking idea’ and visualised the wheel rotating and counting the rotations seen.
The smart people stuff is the trying to do the radius shit.
Correct, I wouldn’t have tried to apply a math equation, I would mentally roll it and count to get the answer. Nothing impressive about that.
Watched the video and was still confused. Had to stare at the cardioid animation on the Wikipedia page for like 10 minutes before I could wrap my head around it.
One thing that helped me intuit the “sidereal” result (4) was to consider what happens as the radius of circle B approaches 0. At least in my mind, it seems pretty clear that A has to undergo at least one rotation.
That said, I am unsure that I would have caught this as a test-taker. Derek’s videos always have some “trick”, putting me on guard, but in a testing scenario I would have seen the answer for 3 with no answer for 4, marked it down, and moved on quickly.
VG video. Confused by the word ‘revolve’? How many times does the Earth ‘revolve’ around the Sun in a year?
But, worse yet, there were THREE correct answers … none listed!
I did not watch this video but did read about this math. Visualize the larger circle unwrapped into a flat line, and the smaller circle sliding along the length of the line so its bottom point is fixed to the line. You’ll see the small circle never rotates. Now slide the small circle with a point fixed onto the large circle in the same way, and you’ll see the small circle makes one complete rotation. That rotation happens in addition to the rotations you get from dividing the larger circumference by the smaller circumference, so the answer is 4 in this case
Satellite operators have to use this equation for orbits.
Wouldn’t it be 3 = 6π/2π ?
if the path had been straight yeah, but the path itself rotates 360 degrees, which gives us an extra rotation
This is the comment that finally enlightened me
This finally made it click. Thanks
Thank you
Now that is mind-bending trickery! Having a degree in applied matha millennia ago did not help…
That’s what you’d think, but there’s an extra rotation involved in the act of the small circle moving around the larger circle rather than along a straight line, so it’s (6π/2π) + 1
I just watched the video, that’s really interesting. Thanks for the explanation
Watch the video, it’s explained.
deleted by creator
This should have been an article. What’s the summary?
I summarized it above, there’s an extra rotation included when the outer circle moves along the inner circle, essentially falling a bit with every roll forward. If the outer circle rolled along a straight line of the same length as the circumference of the inner circle, it would only roll 3 times, but moving around the circle instead adds exactly one extra rotation. That other gent says this is used in calculating orbits too, where you’re also moving forward while constantly falling
I read an article about it. Everybody is doing a shit job of describing what happens. The outer circle naturally makes a full rotation as it travels around the inner one, as the path it follows goes around a full 360°, so that counts as one of the rotations it ends up making, which is in addition to the 3 due to travel around the circumference.
thank you, that was the comment that explained it for me
Thanks for letting me know! It was too frustrating to not share.
deleted by creator
Does not compute
deleted by creator
First you said add the radii together, then you gave an example subtracting them, but either way this is incorrect. You divide the larger radius by the smaller radius and add 1
Not quite. With radius 2 and 3 circles, the outer circle would take 2.5 rotations to complete the revolution. You have to set the first circle radius to 1 (divide both radii by the lesser) and then add the radii to calculate the relative circumference of the circle drawn by the motion of the center of the outer circle, so the answer would be calculated like:
2/2 + 3/2 = 5/2 = 2.5
Removed by mod
deleted by creator
Its not even remotely what you said. Its A/B+1 or A/B-1 for an interior loop.
edit: I didn’t need to be this aggressive. It’s VAGUELY what you said. its (A+B)/B. You have missed the /B part… which is A/B + 1.
in the example you gave, for radius 2 and 3… it would be 3/2 + 1 or 2.5. Not 5 (off by a factor of 2 because /B)
The center travels 2π per rotation but need to travel 8π because the path of the center of the small circle is a circle 4r the radius of the large circle plus the radius of the small circle. It would be three if the center of the small circle traveled along the edge of the larger circle but it’s edge to edge.
deleted by creator
I’m proud to say that I got 4 as the answer in the beginning. HOWEVER, the options threw me off, which made me watch the rest of the video :(
I was like “Hum… That should do like more than 3.5, but 4 at maximum…”
Then he shows options, and I was like “What ? There’s nothing between 3.5 and 4”; then thought about it a bit more, and found Exactly 4 as an answer; then continued to watch the end of the video to see why my calculations were wrong (they wer’nt)
This is crazy interesting!
>/= 1
They didn’t say anything about b’s movements.
This video is recommended by Tournesol:
[38🌻] Veritasium: The SAT Question Everyone Got WrongTournesol is an open-source web tool by a non profit organization, aiming to evaluate the overall quality of the information in videos from community made comparisons, to fight against misinformation and dangerous content.
deleted by creator
There’s one extra-rotation from an external perspective due to the revolution of one around the other. So the formula is r1 / r2 + 1.
This extra-rotation doesn’t appear from the point of view of the circles, or if you consider the circles as two stationary gears
You could just watch the vid you know
Godamn thats a phenominal example of reletivity.
Booooo
This video didn’t give the correct answer in any place reasonable. I just wanna know the answer before you go off on an 18 minute lecture.
To anyone who just wants to know the answer without watching the whole video, the correct answer is 4
https://www.nytimes.com/1982/05/25/us/error-found-in-sat-question.html
He spends the first 5 minutes explaining the answer is 4, but the question was also worded ambiguously that 3 and 1 can also be correct answers.
Maybe watch the video, it’s more interesting than you’d think
How did this video stretch out to 18 mins?
I remember a mindyourdecisions yt video about this from several years ago that showed it in a couple of minutes and why it is n+1.
sorry i don’t remember the url though.It explains the answer is 4 before the 5 minute mark.
Part of the reason is because it goes into the story of the SAT being wrong and a student being the one to catch it, which I found interesting.
After that it mathematically proves it several different ways and then shows how it relates to some real problems in astronomy.